The Benefits of Log Transformations
Strap in tight: a log of fun stuff to follow
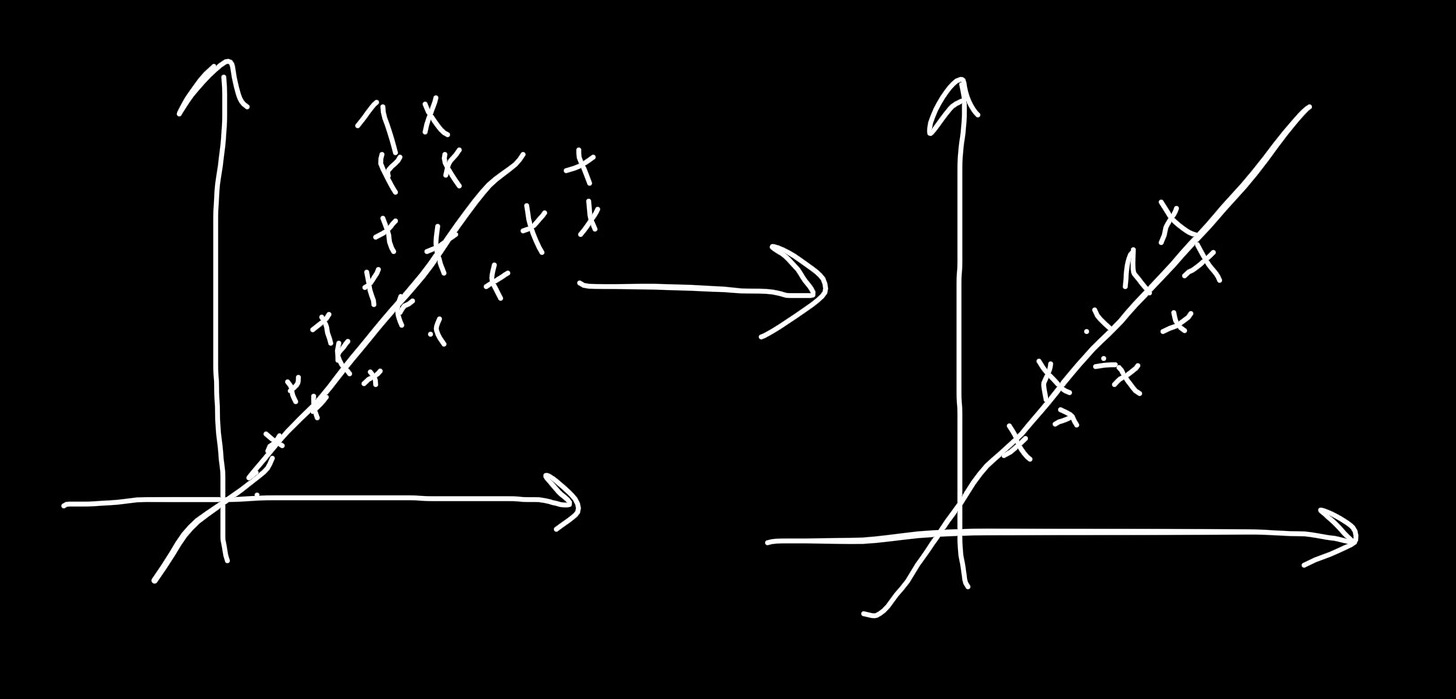
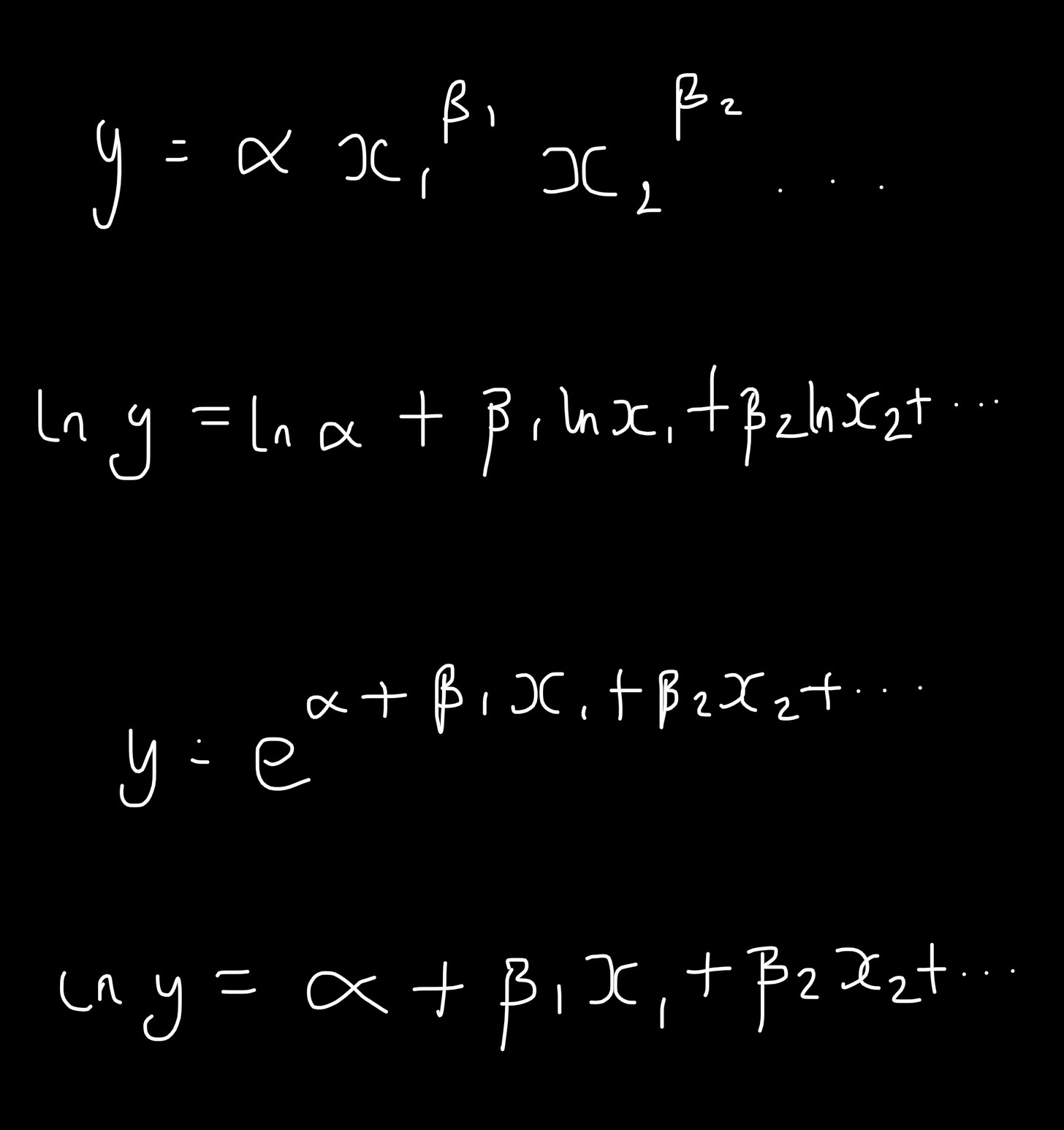1. Linearity. Log models allow for complex, multiplicative relationships to be expressed in linear form Y= C + Mx. More appropriate to fit linear regression models to such transformed data than attempting to explain non-linear relations with linear models.
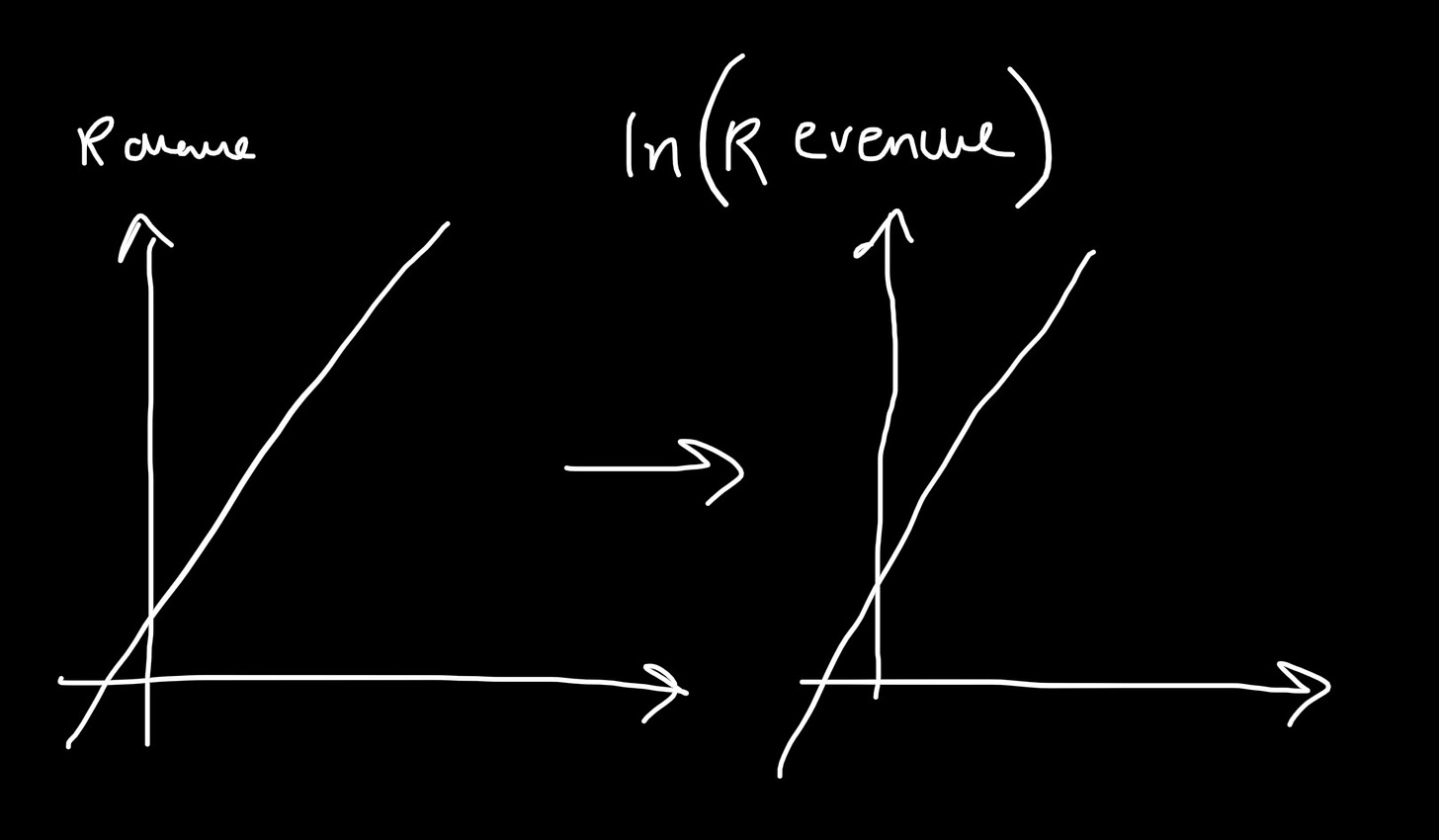
2. Bounded variables. Some variables are bounded. Revenues cannot be negative, nor can height. As a rule, linear models assume variables to be unbounded. OLS lines are not intrinsically-bounded, and fitted to raw data may not make perfect sense. Think E[Revenue] being negative for certain values of the independent variables. Taking log variables extends their values to between negative and positive infinity, resolving this issue.
3. Normalcy. An extension of the former advantage. Skewed or bounded data may be made more normal, potentially improving the utility of tests which assume normalcy.
4. Heteroskedasticity patch. Think of this as crunching data together. Log models can smooth some heteroskedasticity of data and errors. This might improve tests which assume normalcy.
5. Elasticity. Useful for econometrics. By taking partial derivatives, we reveal the effect of the beta coefficients as variables … vary.
Beta coefficients approximately represent:
Log-Log: partial elasticity of dependent variable with respect to X1
Semi-Log x: unit change in dependent variable for % change in X1
Semi-Log y: percentage change in dependent variable for unit change in X1
